Falls Sie die gebogenen Zeiger näher interessieren und Sie nicht vor ein wenig Mathematik zurückschrecken, können sie hier eine einfache Betrachtung finden.

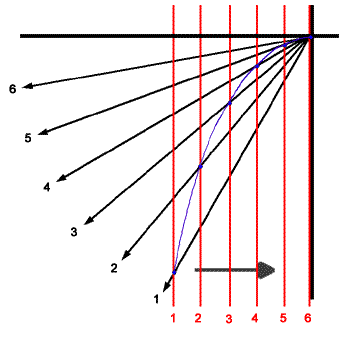
Bei der Entstehung der gezeigten Fotos bewegt sich die abgetastete Zeile von oben nach unten. Im Gegensatz dazu sind die Zeichnungen auf dieser Seite um 90 Grad gedreht, so dass der Scanvorgang von links nach rechts fortschreitet.  Die roten senkrechten Linien im Bild rechts repräsentieren die Position der Zeile in festen Zeitabständen. Die aufsteigenden rot geschriebenen Zahlen bezeichnen den zugehörigen Zeitpunkt. Zu denselben Zeitpunkten ist auch die Position des Sekundenzeigers mit einem schwarzen Pfeil eingezeichnet. Die schwarzen Ziffern geben wieder den Zeitpunkt an. Ein Punkt des Zeigers wird immer an den Schnittpunkten der Liniensysteme zum gleichen Zeitpunkt erzeugt. Die sich ergebenden Schnittpunkte sind mit der blauen Linien verbunden, die dem Bild des Zeigers in gescannten Bild entspricht. 

Um die Kurven analytisch anzugeben, sei das Koordinatensystem gewählt, wie es rechts zu sehen ist. Da die CCD-Zeile (bzw. gleichbedeutend der Spiegel, der das Licht auf die CCD-Zeile lenkt) den als Strecke idealisierten Zeiger in höchstens einem Punkt schneidet, ist es zweckmäßig, die CCD-Zeile in Richtung der x-Achse wandern zu lassen. Dadurch wird der Schnittpunkt von CCD-Zeile und Zeiger y(x) eine Funktion (keine Mehrdeutigkeit). Interessiert man sich nicht für die Position der Zeigerspitzen, kann man statt des Zeigers vereinfachend eine Gerade durch den Ursprung betrachten, die sich mit konstanter Winkelgeschwindigkeit in mathematisch negativer Richtung um den Ursprung dreht.

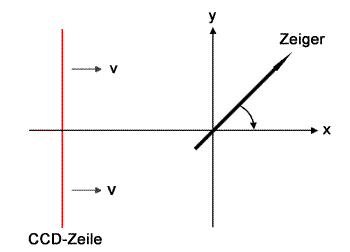
Diese Gerade hat die Form y = m*x

mit der Steigung m = -tan(ω*t - α)

Dabei ist ω die als positiv angenommene Winkelgeschwindigkeit, t die Zeit und α der Winkel des Zeigers zum Startzeitpunkt t=0. Man könnte durch geschickte Festlegung des Startzeitpunktes immer α=0 erreichen, aber das würde bei der konkreten Berechnung keine Vorteile schaffen. Das Minus-zeichen vor dem Tangens sorgt  für die Drehung in negativer Richtung. Alternativ hätte man auch ein negatives ω annehmen können.

Die senkrechte Zeigerposition kann so nicht beschrieben werden. In diesem Grenzfall gibt es keinen Schnittpunkt, es sei denn, der Scanner steht gerade beim Koordinatenursprung (über der Zeigerachse). Dann ist die ganze  y-Achse eine Schnittgerade.

Die Bewegung der CCD-Zeile erfolgt mit konstanter Geschwindigkeit v:

x = v*t + x₀

Startet der Scanner bei t=0, dann ist x₀ gerade die Abstand der Zeigerachse vom Rand des Scanners.

Elimination der Zeit t liefert die Ortskurve:

y(x) = -x*tan((x-x₀)*ω/v - α) = -x*tan((x*ω/v - β)

wobei β =  x₀*ω/v + α ist.

Interessiert man sich für die Enden der Kurvenstücke bei einem realen Zeiger der Länge R, so muss man den x-Wert des Zeigerendpunktes betrachten:

x = R*cos(ω*t - α) Dieser Punkt wird vom Scanner erfasst, wenn

 v*t + x₀ = R*cos(ω*t - α),

was man numerisch nach t auflöst. Die Koordinaten zum Zeitpunkt des Schnittes t_s sind:
x =   R*cos(ω*t_s - α)
y = - R*sin(ω*t_s - α)