Das Stereomikroskop MBS-10 - Notiz zu den technischen Daten

Brennweiten
Zu dem Stereomikroskop MBS-10 von LOMO lagen mir leider kaum Daten vor. Lediglich aus einer Werbung konnte ich entnehmen, dass die Brennweite des Objektivs fO=90mm beträgt. Das entspricht in etwa meinen Messungen des Arbeitsabstands. Im Folgenden gehe ich von dieser Brennweite aus. Kleinere Abweichungen bei den abgeleiteten Werten sind auf Grund dieser Unsicherheit und von Fehlern bei Längenmessungen möglich. Falls ein Besucher dieser Seiten über genauere Daten verfügt, wäre ich für eine kurze Mitteilung dankbar.


Rechts ist ein Stereomikroskop nach dem Fernrohrprinzip samt Fototubus dargestellt. Das Objekt befindet sich im Fokus des Objektivs, das deshalb ein Bild des Objekts im Unendlichen entwirft.  (Unendlichoptik).

Die Tubuslinsen erzeugen im Abstand ihrer Brennweite fT daraus ein reelles Bild, welches  mit einem Okular betrachtet werden kann. Mittels einer Schaltwalze können Galileifernrohre in jeweils beiden Orientie-rungen eingeschwenkt  werden. Dies ermög-licht verschiedene Abbildungsmaßstäbe. Beim MBS-10 ist ohne zusätzliche Optik zwischen Objektiv und Tubuslinse ein Ver-größerungsfaktor k=2 (Abbildungsmaßstab ohne Okularvergrößerung) am Revolver angegeben. Dieser Abbildungsmaßstab be-rechnet sich aus den Brennweiten nach der Beziehung:

k = fT/fO

Mit fO=90mm und k=2 folgt die Brennweite der Tubuslinsen zu fT=180mm. Dies ist zugleich die optische Tubuslänge.
 

Galilei-System
Die Vergrößerungsfaktoren der Galilei-Systeme lassen sich leicht angeben. Wird der gesamte Abbildungsmaßstab bei ein-gelegtem Galilei-Fernrohr zum Beispiel k=4, dann bewirkt das Galilei-Fernrohr offenbar einen zusätzlichen Vergrößerungsfaktor von 2. Dreht man den Revolver um 180 Grad, so dass das Galilei-Fernrohr umgekehrt einge-setzt ist, bewirkt es einen Vergrößerungs-faktor von 1/2 (Verkleinerung). Damit ergibt sich die Gesamtvergrößerung zu k=2*1/2 =1. Ganz analog ergeben sich die Werte für die anderen Stellungen des Galilei-Wechslers. Bei k= 7 bewirkt das Galilei-Fernrohr einen Faktor von 3,5, bei k=0,6 von 0,3. Das ist in etwa invers zueinander.

 

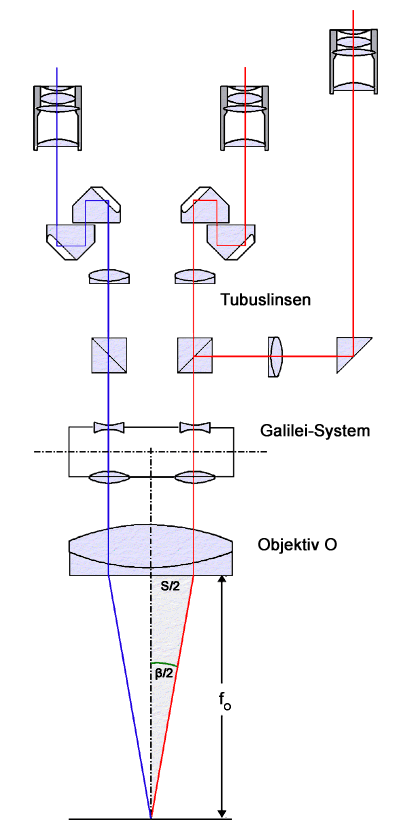
Strahlengang zu Stereomikroskop nach dem Fernrohrprinzip samt Fototubus - Bild ist zum Verständnis des Textes sehr hilfreich

Konvergenzwinkel
Für die Räumlichkeit der visuellen Beobachtung und für die Stereofotografie ist der Konvergenzwinkel β wesentlich, unter dem das Objekt gesehen wird.  Dieser ist einfach abschätzbar. Der Abstand der beiden Teilstrahlengänge  zwischen Objektiv und Umkehrprismen beträgt beim MBS-10 gemessene 20mm.  Dies entspricht der Stereobasis S. Daraus, sowie der Objektivbrennweite fO=90mm ergibt sich der halbe Konvergenzwinkel zu :

β/2 = atan(S/[2*fO]) = 6,34°  (siehe hellgrau hinterlegtes Dreieck)

Der Konvergenzwinkel β liegt deshalb bei 13°. Ein Mensch mit einem Augenabstand von 65mm sieht einen Gegenstand in knapp 30cm Entfernung unter diesem Winkel.


Numerische Apertur
Bei einem "gewöhnlichen" Mikroskop werden verschiedene Objektive mit unterschiedlichen nume-rischen Aperturen für die jeweiligen Vergrößerungsstufen eingesetzt. Wenn man einmal von Konverter-linsen absieht, besitzt dieses Stereomikroskop nur ein Objektiv und arbeitet mit einem Arbeitsabstand. Unterschiede in der numerischen Apertur bei den verschiedenen Vergrößerungsstufen kommen durch verschiedene Eintrittspupillen zustande. Diese sind durch die Linsendurchmesser der Eintrittslinsen in das Galilei-System oder die Blendenwirkung der Bohrungen (falls keine zusätzliche Optik eingelegt wird)  gegeben. Ein ungefähres Ausmessen dieser Durchmesser am MBS-10 liefert etwa 4mm für die Vergrößerungsstufe 0,6, 6mm für die Vergrößerungsstufe 1x, 14mm für die Vergrößerungsstufe 2x und schließlich 15mm für die Vergrößerungsstufen 4x und 7x. An dieser Stelle möchte ich darauf hinweisen, dass ich früher (Homepage bis zum 25.02.2009) von einem Durchmesser von 6mm für die Vergrößerungsstufe 0,6 ausgegangen war. Hr. Jürgen Schrodt hat mich dankenswerterweise darauf hingewiesen, dass der Durchmesser der Eintrittslinse des Galilei-Wechslers durch eine Blende im Linsensystem eingeschränkt wird. Sie ist beim Blick durch die Linse als dunkler Ring erkennbar.

Mit der Brennweite fO=90mm kann man die numerischen Aperturen berechnen:
k  Ø    nA
0,6 4mm 0,022
1 6mm 0,033
2 14 0,077
4 15 0,083
7 15 0,083

Von kleinen, wenig relevanten Unterschieden abgesehen, gibt es drei numerische Aperturen, gerundet 0,02, 0,03 und 0,08. Insbesondere bei der größten Vergrößerungsstufe 7x macht es sich bemerkbar, dass die Auflösung nur geringfügig diejenige der nächst kleineren Stufe 4x übertrifft. Bei den mitgelieferten Okularen mit einer 14fachen Vergrößerung wird eine Gesamtvergrößerung von 98 erreicht, die die förderliche Vergrößerung (das 500 bis 1000fache der nA) schon deutlich überschreitet. Im Gegensatz dazu wird bei der niedrigsten Vergrößerungsstufen k=0,6 die förderliche Vergrößerung nicht erreicht. Unschärfen aufgrund der optischen Abbildung sind  mit bloßem Auge nicht erkennbar.


Auflösung
Nach der Airyschen Betrachtungsweise ergibt sich der kleinste auflösbare Abstand zweier Punkte eines selbstleuchtenden Objektes durch:

d = 1.22*λ/(2*nA)

Bei einer Wellenlänge von λ=550nm (grünes Licht) erhält man folgende Werte:
k  nA      d
0,6 0,022 0,0153mm
1 0,033 0,0102mm
2 0,077 0,0044mm
4 0,083 0,0040mm
7 0,083 0,0040mm

Zwei Beispiele zur Anwendung: Betrachten wir den Vergrößerungsfaktor k=1 und damit d=0,0102mm. Wie bereits geschildert, wird bei der beschriebenen einfachen Anpassung der Coolpix 990 lediglich ein 12mm breiter Ausschnitt aus dem reellen Zwischenbild auf den CCD-Chip der Kamera abgebildet. Wegen k=1 entspricht dies auch einer Länge im Objektraum von 12mm. Diese Länge besteht aus 12/0,0102=1180 unterscheidbaren Punkten. Kann man durch sehr geschickte Adaption 20mm des Zwischenbildes ausnutzen, wächst die Zahl unterscheidbarer Punkte auf rund 2000.

Führt man diese Überlegung für k=4 aus, so kann man zwar hier bereits Punkte mit einem Abstand von d = 0,004mm auflösen, aber auch der sichtbare Bereich in der Objektebene reduziert sich. Aus 12mm bei k=1 werden 12/4mm = 3mm bei k=4. Daher bilden nur noch 3/0,004 = 750 Punkte die sichtbare Breite. Erreicht man wieder eine Abbildung von 20mm im Zwischenbild, so steigt diese Zahl auf 1250 Punkte.

Wenn man diese Punkte in einem Digitalbild auflösen will, muss nach dem Abtasttheorem von Shannon und Nyquist die Quantisierung doppelt so fein sein, wie die maximal mögliche Signalfrequenz (hier "Ortsfrequenz"). Etwas lapidar formuliert, benötigt man für ein Beugungsscheibchen der Breite d mindestens zwei Pixel. Die Kamera Nikon Coolpix 990 mit ihren 2.048x1.536 Bildpunkten kann deshalb maximal 1024 Punkte in der Bildbreite trennen. Bei der Aufnahme eines 12mm breiten Ausschnittes des Zwischenbildes ist die Kamera bei k=1 knapp unter der wünschenswerten Auflösung, für höhere k jedoch gut ausreichend. Umgekehrt bedeutet das, die Kamera liefert bei größeren Abbildungsmaßstäben kein optimal scharfes Bild, selbst wenn das Objekt sehr dünn und exakt fokussiert ist. Eine höhere Pixelzahl kann die Bildqualität dann nicht mehr verbessern.

Aus der Zahl der unterscheidbarer Punkte im Zwischenbild erkennt man, dass in einer besseren Adaption deutliches Optimierungspotenzial steckt. Damit man dies auch wirklich nutzen kann, muss die Kamera entsprechend hoch auflösend sein.


Schärfentiefe
Die Schärfentiefe besitzt einen geometrisch-optischen und einen wellenoptischen Anteil. Bei visueller Beobachtung kommt die Akkomodationstiefe hinzu, die bei fotografischen Aufnahmen keine Rolle spielt und deshalb hier nicht näher betrachtet sei. Für die theoretische Ableitung empfehle ich das entsprechende Kapitel aus "Moderne Methoden der Lichtmikroskopie" von G. Göke. Hier sei nur das Resultat der Schärfentiefe t angegeben:

t = 0,15mm/(nA*v) + λ/(2*nA2)

Dabei sind nA die numerische Apertur, v die Gesamtvergrößerung (einschließlich Okular) und λ die Wellenlänge des Lichtes. Geht man wieder von der Wellenlänge  λ=550nm aus und nimmt ein 8x-Okular an, so berechnet man mit den vorher bestimmten numerischen Aperturen folgende Werte:
 
k v      t
0,6 4,8 1,96 mm
1 8 0,81 mm
2 16 0,17 mm
4 32 0,10 mm
7 56 0,07 mm

 

Bezug zur Makrofotografie
Für den Kenner der Makrofotografie mag es interessant sein, die Begriffe der Fotografie zu verwenden, also von der Brennweite des Fotoobjektivs und Blenden zu sprechen.


Dazu muss man die Begriffe der Mikroskopie auf die der Fotografie übertragen. Betrachten wir zu diesem Zweck das Stereomikroskop ohne Galilei-System in Analogie zum Fotoapparat. Dann entsprechen das Objektiv des Stereomikroskops und die Tubuslinse zusammen dem Fotoobjektiv, denn erst diese beiden optischen Komponenten entwerfen des reelle Bild. Im strengen Sinne ist das, was oben als Objektiv des Stereomikroskops bezeichnet wurde, kein Objektiv, denn es wird nicht dazu verwendet, ein reelles Bild zu erzeugen. Man kann es mit der Tubuslinse gedanklich zu einem "echten" Objektiv zusammenfassen. Für eine Linse der Brennweite f gilt bekanntlich:

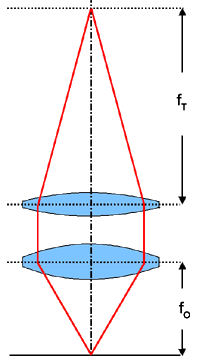
1/f = 1/b + 1/g

wobei b die Bildweite und g die Gegenstandsweite ist. Ersetzt man in nebenstehender Skizze beide Linsen durch eine einzige, so muss  fO = g und fT = b sein. Nach Einsetzen und Auflösen folgt für die Brennweite:

f = fO*fT /(fO  +  fT)

Die Brechkräfte der beiden Linsen addieren sich wie bei zwei dünnen, nahe zusammen stehenden Linsen. Im Fall des MBS-10 berechnet man f = 60mm. Ein Mikroskop mit Endlichoptik und dieser Objektivbrennweite oder ein Fotoobjektiv besitzt exakt dieselben Eigenschaften.

Ohne Galilei-System (k=2, Durchmesser der Blende 14mm) erhält man dann den Blendenwert 60mm/14mm = 4,3. Das ist auch die Lichtstärke des Objektivs beim Abbildungsmaßstab 2:1.

Für die Definition der Schärfentiefe wird in der Fotografie eine zulässigen Unschärfe von 1/1000-stel der Bildbreite zugrunde gelegt, was beim Diafilm etwa 0,03mm ausmacht. Bei einer nutzbaren Breite des reellen Zwischenbildes von 12mm kann man analog einen Unschärfekreis von u=0,012mm an-setzen. Bei der Auflösung der Coolpix 990 entspricht dieser Durchmesser dem 2-fachen Abstand der Pixel. Der maximal sinnvolle sinnvolle Blendenwert wird ebenfalls über diesen Unschärfekreis definiert. Sie ist erreicht, wenn die beugungsbedingte Unschärfe (Radius des Airy-Scheibchens) die Größe des Unschärfekreises erreicht hat. Diese förderliche Blende berechnet sich mit u=0,012mm und bei einer Wellenlänge von λ=550nm zu:

u/(1,22*λ*[k+1]) = 0,012mm/(1,22*550nm*3) = 5,96

(Zur Formel siehe "Fotoschule" von Martin Sigrist und Erwin Stegmann)
Die förderliche Blende ist nicht allzu weit von der oben berechneten Blende des Stereomikroskops bei k=2 entfernt. Ein Verringern des Blendendurchmessers, also Erhöhen des Blendenwertes wird zwar die Schärfentiefe erhöhen, aber schnell die beugungsbedingte Unschärfe in Erscheinung treten lassen. Der niedrige Wert für die förderliche Blende mag überraschen. In Tabellen zu Makrofotografie findet man beim Abbildungsmaßstab 2:1 den Blendenwert 16. Man muss aber bedenken, dass diese Tabellen sich am Diaformat mit einer Breite von 36mm und daher an einem dreimal so großen Unschärfekreis orientieren. Ein Kameragehäuse am Fototubus mit Filmebene im reellen Zwischenbild erreicht fast die Ausleuchtung des Diaformats. Hier könnte man noch etwas abblenden bis zum Erreichen der förder-lichen Blende. Eine bessere Adaption der Digitalkamera würde ebenfalls einen höheren Wert für die förderliche Blende bedeuten.
 
 

Hinweis zur Skizze: Die Zeichnung ist vereinfachend und nicht maßstäblich. Die Bauweise des achromatischen Objektivs sowie der Okulare ist mangels Kenntnis der optischen Details des MBS-10 willkürlich gewählt. Im Strahlengang ist das Objektiv durch eine Linse ersetzt, deren Nodalpunkt an der Eintrittslinse angenommen wurde. Bei einem Stereomikroskop nach dem Fernrohrprinzip haben die bildaufrichtenden Prismen zusätzlich die Aufgabe, aus dem parallelen Strahlengang die natürliche Konvergenzstellung der Augenachsen zu erzeugen, was nicht dargestellt wurde.  Diese bewussten Vereinfachungen spielen bei den obigen Überlegungen keine Rolle.