Wie groß ist nun die Vergrößerung die man mit dem Makrokonverter erreicht und welche Gegenstandsweite ergibt sich? Wie hoch ist die Auflösung? Diese Fragen sollen nun beantwortet werden.

Brennweite und Brechkraft der Lupe
Auf der Lupe ist eine Vergrößerung angegeben, im Fall meiner Lupe 10x. Bei richtigen Gebrauch der Lupe wird der zu betrachtende Gegenstand in den Brennpunkt der Lupe gebracht. Der Betrachter sieht ihn dann mit entspannten Blick, d.h. sein Auge ist auf unendliche Entfernung akkomodiert. Der Gegenstand erscheint dem Betrachter unter einem größeren Winkel, als er ihn ohne Hilfsmittel in "deutlicher Sehweite" sieht, wobei die deutliche Sehweite zu 25 cm definiert wurde. Das Verhältnis dieser Sehwinkel ist die Vergrößerung der Lupe. Für die Lupe kann man die Beziehung herleiten:

v = d/f_L

wobei v die Vergrößerung, d = 250mm die "deutliche Sehweite" und f_L die Brennweite der Lupe ist. Ist die Vergrößerung gegeben, so ergibt sich die Brennweite zu:

f_L = 250mm/v

Bei einer Lupe mit der Vergrößerung 10x ist die Brennweite 25mm.

Bei Nahlinsen wird nicht die Brennweite, sondern die Brechkraft (Brechkraft = 1/Brennweite) angegeben. Die Brechkraft besitzt die Einheit 1/m, die man als Dioptrie bezeichnet. Daher ist die Brechkraft der verwendeten Lupe

1/(0,025m) = 40 Dioptrien
 

Brennweite der Kamera mit Makrokonverter
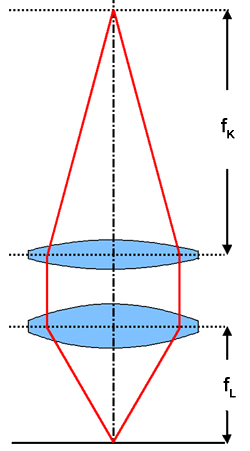
Im Bild rechts ist die Kamera mit vorgesetzter Lupe schematisch dargestellt. Lupe und Kameraobjektiv sind jeweils zu einer Linse zusammengefasst. Die Brennweite des Kameraobjektivs sei f_k.  Ein betrachteter Punkt des Motivs befinde sich im Brennpunkt der Lupe. Das von ihm ausgehende Licht wird durch die Lupe in ein paralleles Strahlenbündel verwandelt, welches vom Objektiv der Kamera deren Brennpunkt abgebildet wird. Für eine Linse der Brennweite f gilt bekanntlich:

1/f = 1/g + 1/b

wobei b die Bildweite und g die Gegenstandsweite ist. Ersetzt man in nebenstehender Skizze das Kameraobjektiv und die Lupe durch ein einziges Objektiv, so muss f_L = g und  f_K = b sein. Damit ist:

1/f = 1/f_L + 1/f_K

Die Brechkräfte der beiden Linsen addieren sich wie bei zwei dünnen, nahe zusammen stehenden Linsen. Dies ist eine Folge der Unendlichoptik. Das Licht jedes Punktes, der sich in der vorderen Brennebene des Makrokonverters befindet, wird von diesem in ein paralleles Strahlenbündel umgewandelt. Das Makroobjektiv entwirft deshalb ein Bild des Objekts im Unendlichen.

Auflösen des obigen Ausdrucks nach f ergibt die Brennweite:

f = f_L*f_K /(f_L  +  f_K)

Viele Digitalkameras besitzen ein Zoom-Objektiv. Bei der erwähnten, von mir verwendeten Coolpix 990 kann der Brennweitenbereich von 8,2mm bis 23,4mm (Brennweite nicht umgerechnet in analoge Größen beim Kleinbildformat) eingestellt werden. Setzt man eine Lupe mit Brennweite 25mm davor, deckt das gesamte System einen Bereich von f = 6,17mm bis f = 12,09mm ab.

Abbildungsmaßstab
Wesentlich ist, dass man bei den oben berechneten Brennweiten sehr nahe an die Motive herankommt, denn bei der beschriebenen Anordnung befindet sich das Motiv im Brennpunkt der Lupe. Der Abbildungsmaßstab β des Objektivs ist gegeben durch das Verhältnis von Bildgröße zu Gegenstandsgröße. Dieses ist gleich dem Verhältnis von Bildweite zu Gegenstandsweite, also

β = b/g = f_K /f_L

Bei den oben angegebenen Daten (f_L = 25mm, f_K = 8mm bis 24mm) ergibt sich der Abbildungsmaßstab von 8,2/25 bis 23,4/25. Man erreicht also etwa einen Abbildungsmaßstab von 1.

Üblicherweise wird der Abbildungsmaßstab als Verhältnis angegeben, wobei die Gegenstandsgröße gleich 1 gesetzt wird. Im obigen Beispiel nimmt β die Werte von ca. 1:4 bis 1:1 an. Das sind eigentlich keine beeindruckenden Werte, jedoch muss man beachten, dass der Gegenstand nicht auf einen Kleinbildfilm, sondern auf einen wesentlich kleineren Sensor (CCD- oder CMOS-Chip) abgebildet wird. Die Coolpix 990 besitzt einen CCD-Chip mit einer Diagonalen von 0,56'' = 14,2mm, die genutzte Aufnahmefläche ist allerdings kleiner. Der Umrechnungsfaktor auf Kleinbildgröße beträgt etwa 4,8. Entsprechend wird auch in den Datenblättern zur Kamera eine auf Kleinbildfilm umgerechnete Brennweite von 38mm bis 115mm angegeben. Will man wissen, welchen Abbildungsmaßstab man bei einem Kleinbildfilm bräuchte, um dieselben Verhältnisse wie bei der Digitalkamera zu bekommen, kann man den  Abbildungsmaßstab bei der Digitalkamera mit dem Größenverhältnis multiplizieren. Sind bei der Digitalkamera die auf Kleinbildfilm umgerechneten Brennweiten angegeben, kann man auch einfach diese in das Verhältnis f_K/f_L einsetzen. In meinem Fall erreicht man bei Wahl der höchsten Brennweite einen äquivalenten Abbildungsmaßstab von 115mm/25mm = 4,6:1. Ein Motiv der Breite von gut 8mm (etwas mehr als die Breite des effektiven CCD-Sensors) wird formatfüllend abgebildet. Gibt man das Digitalbild auf Bildschirm oder Drucker mit einer Breite von z.B. 16cm aus, dann bedeutet das eine 20-fache Vergrößerung.

Vignettierung
Montiert man die Lupe auf die beschriebene Weise vor die Kamera, stellt sich schnell heraus, dass im unteren Bereich der Brennweite das Bild nicht vollständig nutzbar ist, sondern nur ein kreisförmiger Bereich in der Bildmitte. Umgeben ist er von einer schwarzen Abschattung durch den Rand der Lupe.

Dieser weicht mit wachsender Brennweite zurück. Erst bei einer Brennweite, die etwas oberhalb von fK=13,5mm liegt, verschwindet diese so genannte Vignettierung vollständig aus dem Bildfeld. Als Beispiel für die Vignettierung ist links ist eine Aufnahme mit fK=8,2mm und rechts mit fK = 13,5mm gezeigt.

In der vorgestellten Ableitung des Abbildungsmaßstabs spielt der Abstand von Objektiv zum Makrovorsatz keine Rolle und er geht nicht die Berechnungsformel ein. Das ist eine Folge der Unendlichoptik, also des parallelen Strahlenganges zwischen den optischen Teilsystemen. Für die Größe des sichtbaren Bereiches ist dieser Abstand aber entscheidend. Um die Vignettierung gering zu halten, muss die Lupe möglichst nahe an das Kameraobjektiv gebracht werden.

Die Vignettierung ließe sich mit einer Lupe größeren Durchmessers verringern oder sogar verhindern. Bei Verwendung der Kamera Coolpix 990 ist eine größere Lupe nicht erforderlich. Bei Objektivbrennweiten unter 13,5mm kann der Abbildungsmaßstab auch ohne Makrokonverter mit der eingebauten Makrofunktion erreicht werden. Bei größeren Brennweiten als 13,5mm tritt hingegen keine Vignettierung mehr auf. Zudem sind hochwertige Lupen mit großen Durchmessern teurer und schwerer erhältlich.

Auflösung und Blende
Die erreichbare Auflösung des Bildes ist nicht nur durch die Pixelzahl des Sensors, sondern auch durch die abbildende Optik begrenzt. Es ist nicht sinnvoll, die Pixelzahl zu erhöhen, wenn die Optik nicht eine entsprechende Auflösung bieten kann.

Zur groben Abschätzung der beugungsbegrenzten Auflösung beschränke ich mich auf die größte Brennweite (f_K = 23,4mm) und damit größte Vergrößerung. Exemplarisch betrachte ich zwei weit auseinander liegende Blendenwerte, nämlich 4 und 11. Der Blendenwert ist das Verhältnis von Brennweite zu Blendendurchmesser. Da die Blende der Quotient von Brennweite zum Durchmesser der "wirksamen Öffnung" ist, kann man diesen Durchmesser berechnen. Die Blendenangaben beziehen sich natürlich auf die Brennweite f_K der Kamera. Der Blendenwert 4 entspricht einem Blendendurchmesser von 5,85mm und der Blendenwert 11 einem Blendendurchmesser von 2,13mm. Entscheidend für die beugungsbegrenzte Auflösung ist die numerische Apertur nA. Im Medium Luft ist dies einfach der Sinus des halben Öffnungswinkels. Für nA ergeben sich die Werte von 0,11 (Blendenwert 4) und 0,043 (Blendenwert 11). Dies sind sehr gute Werte, wenn man bedenkt, dass die förderliche Vergrößerung, über die man nicht hinausgehen sollte das 500- bis 1000-fache der numerischen Apertur beträgt. Oberhalb der förderliche Vergrößerung werden keine neuen Details sichtbar. Man spricht dann von leerer Vergrößerung. Die Aperturen sind beachtlich im Vergleich zu einem Stereomikroskop, insbesondere beim Blendenwert 4. Der Grund ist darin zu sehen, dass bei vergleichbarem Blendendurchmesser der Arbeitsabstand mit 25mm sehr klein in Relation zum Arbeitsabstand bei einem typischen Stereomikroskop ist.

Der kleinste auflösbare Abstand zweier Punkte eines selbst leuchtenden Objektes ist gegeben durch:

d = 1.22*λ/(2*nA)

Bei einer Wellenlänge von λ=550nm (grünes Licht) erhält man bei nA=1,1 einen auflösbarer Abstand von d=0,003mm und bei nA=0,043 von d = 0,008 mm. Bei einer abgebildeten Breite des Objekts von 8mm können deshalb rund 2860 Bildpunkte bzw. 1040 Bildpunkte unterschieden werden. Damit auch die Kamera diese Punkte unterscheiden kann, muss sie nach Abtasttheorem von Shannon und Nyquist doppelt so viele Pixel aufweisen (siehe Seite zum MBS-10). Deshalb würde man 5720 bzw. 2080 Pixel in der Bildbreite benötigen, um die optische Information voll auszunutzen. Die Nikon Coolpix 990 besitzt 2.048x1.536 Bildpunkte, was bedeutet, dass sie zwar nicht in jedem Fall die Bildinformation ausnutzt, aber in diesem Blendenbereich ein scharfes Bild liefert. Ihre Auflösung wird also nicht verschenkt und in diesem Sinne passt sie zu den erreichbaren Auflösungen. Eine Kamera mit höherer Pixelzahl würde andererseits bei niedrigen Blendenwerten eine Verbesserung der Auflösung im Bild ermöglichen.

Die genannten theoretischen Grenzen der Auflösung wird man sicher nicht erreichen, sei es wegen ungenauer Fokussierung, Verwackeln oder Abbildungsfehlern. Dennoch schneidet der einfache Makrokonverter gut im Vergleich zum Stereomikroskop ab. Will man "nur" fotografieren, ist dies eine preisgünstige und einfache Möglichkeit.
 

Schärfentiefe
Bei den bisherigen Betrachtungen zur Auflösung ist die Unschärfe auf Grund einer endlichen Tiefe des Objekts nicht berücksichtigt. Sie kommt zur beugungsbedingten Unschärfe noch hinzu. Eine quantitative Berechnung der Schärfentiefe möchte ich hier nicht durchführen. Wen dies interessiert, der möge sich die Berechnung im Abschnitt "technische Daten" zum Stereomikroskop ansehen. Es gibt auch praktisch zu handhabende Tabellen. Wichtig für die praktische Arbeit ist, dass die Schärfentiefe mit dem Blendenwert wächst. Selbst beim Blendenwert von 11 ist die beugungsbegrenzte Unschärfe akzeptabel (s.o.), so dass ich immer versucht habe, einen relativ hohen Blendenwert (8 oder 11) zu wählen. Das erfordert auch einen ausreichende Beleuchtungsstärke, weil Digitalkameras oft keine langen Belichtungszeiten erlauben.