Abbildungsmaßstab und Vergrößerung

Abbildungsmaßstab Nachfolgend sollen der Abbildungsmaßstab und die visuelle Vergrößerung des Makroskops behandelt werden. Der Strahlengang des Makroskops ist mit den wichtigsten Längenbezeichnungen im Bild rechts dargestellt. Damit Punkte der Objektebene scharf in die Zwischenbildebene abgebildet werden, muss zwischen Bildweite (b), Gegenstandsweite (g) und Brennweite (f) die Abbildungsgleichung erfüllt sein: 1/g + 1/b = 1/f Der Abbildungsmaßstab (m) ist definiert als Verhältnis von Bildgröße zu Gegenstandsgröße in der Zwischenbildebene: m = B/G Aus der Ähnlichkeit der Dreiecke, die vom Mittelpunktstrahl, der optischen Achse und den Stecken, die den Gegenstand und sein Bild repräsentieren, gebildet werden, entnimmt man: m = B/G = b/g Mit Hilfe der Abbildungsgleichung kann man g eliminieren und damit den Abbildungsmaßstab durch Brennweite und Bildweite ausdrücken: m = b*(1/g) = b*(1/f - 1/b) = (b - f)/f = x/f Dabei wurde die Auszugsverlängerung x als  x = b - f definiert.

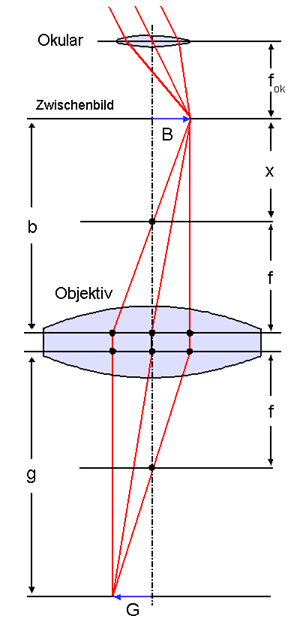Als Faustregel kann man sich merken, dass der Abbildungsmaßstab gerade 1 wird, wenn die Auszugsverlängerung gerade gleich der Brennweite ist. Dann sind Bildweite und Gegenstandsweite gleich groß, und zwar gleich der doppelten Brennweite.

Da die Brennweite auf fast jedem Objektiv angegeben ist, kann man in der Regel den Abbildungsmaßstab berechnen, wenn man die Auszugsverlängerung kennt. Diese ist zwar auf der Skala jedes Balgengerätes angegeben, berücksichtigt aber nicht die Unterschiede im Lichtweg zwischen Kameragehäuse und dem aufgesetzten Tubus. Nur, wenn "zufällig" der Lichtweg im Tubus zwischen dessen Auflage und seiner Zwischenbildebene gerade dem Auflagemaß der Kamera (Abstand vom Auflageflansch des Bajonetts bis zur Film- oder Chipebene) entspricht, sind die Skalenwerte am Balgengerät korrekt. Auch die Retrostellung eines Objektivs führt zu Abweichungen von der abgelesenen Auszugsverlängerung. Um aus dem abgelesenen Wert die tatsächliche Auszugsverlängerung zu bestimmen, muss man – etwas vereinfacht ausgedrückt - die Differenzlänge zwischen dem Lichtweg im Tubus und Kameragehäuse addieren. Diese Korrekturlänge kann man mit einer einzigen Messung ermitteln. Dazu legt man ein Objektmikrometer oder ein anderes flaches Objekt bekannter Länge unter das Makroskop und stellt den Balgen auf einen bestimmten Auszug ein, wobei sich der größte Auszug empfiehlt, weil man damit die genauesten Ergebnisse erwarten kann. Das Makroskop wird durch Höhenverstellung fokussiert. In das Okular wird ein Okularmikrometer eingelegt. Sind das Okularmikrometer und das Objektmikrometer gleichzeitig scharf zu sehen, dann befindet sich das Okularmikrometer in der Zwischenbildebene und die Beziehung

x = f*m

ist anwendbar.
 

Den Abbildungsmaßstab m = B/G kann man unmittelbar beim Blick durchs Okular bestimmen. In dem Beispiel rechts wurde mit dem Zeiss-Tubus und einem 50mm Normalobjektiv aufgenommen. Oben ist das Objektmikrometer zu sehen (lange Striche im mm-Abstand) und unten das Okularmikrometer.

Eine Gegenstandsgröße von 2mm (obere Skala) wird im Zwischenbild auf 9,08mm (untere Skala) vergrößert, was einem Abbildungsmaßstab von

m = 9,08/2 = 4,54 entspricht.

Da ein Normalobjektiv mit einer Brennweite 50mm verwendet wurde, ist

x = 227mm

Am Balgengerät war dabei der höchste Auszug mit einem Skalenwert von 130mm angezeigt, so dass man zum Wert am Balgengerät immer 97mm hinzuzählen muss.

Ist die Brennweite des Objektivs nicht oder nicht genau bekannt, wie etwa bei einem Mikroskopobjektiv, so kann man die Brennweite und die Korrektur zur Auszugsverlängerung mit zwei Messungen bestimmen, wie in einer Notiz näher ausgeführt ist.

Anmerkung: Als Objektmikrometer wurde das Mikrometerplättchen aus einem MBS-10 Okular verwendet. Das Bild ist beim höchsten Abbildungsmaßstab aufgenommen und zeigt schon deutliche Abbildungsfehler. Man erreicht deutlich spürbar die Auflösungsgrenze des Makroskops und auch eine Kissenverzerrung ist nicht zu leugnen. Wenn man Wert auf derart hohe Abbildungsmaßstäbe legt, sollte man sich nach einem Lupenobjektiv umschauen.

Vergrößerung bei visueller Beobachtung
Betrachtet man einen Gegenstand mit einem Okular, so erscheint dem Beobachter das Objekt unter einem anderen Winkel, als wenn es sich in einer bestimmten Bezugsentfernung vor dem Auge des Betrachters befände. Das Verhältnis dieser Winkel wird als Vergrößerung des Okulars bezeichnet. Als Bezugsweite wird dabei die "deutlicher Sehweite" von d = 250mm gewählt. Zwischen der Vergrößerung des Okulars v_ok und seiner Brennweite fok besteht die Beziehung:

v_ok = d/ f_ok

Wird mit dem Okular das Zwischenbild betrachtet, so erscheint in dem zusammengesetzten System das Objekt ebenfalls vergrößert, wobei sich die gesamte Vergrößerung sich als

v = v_ok * m = v_ok * x/f = d*x/(f_ok * f)

ergibt.

Bei einem 10x-Okular erhält man im obigen Beispiel eine rund 45-fache Vergrößerung. Das Objekt erscheint unter dem 45-fachen Sehwinkel im Vergleich zur Betrachtung in 25cm Entfernung.

Setzt man einen kompletten Tubus auf das Balgengerät, so muss man bedenken, dass manche Tuben eine Eigenvergrößerung besitzen, die man als Tubusfaktor v_T bezeichnet.

Wenn der Tubusfaktor von 1 abweicht, ist obiger Ausdruck zu erweitern:

v = v_T * v_ok * m = v_T * v_ok * x/f

Abbildungsmaßstab und Sehfeld einer Kamera
Eine Kamera bildet einen begrenzten Teil des Zwischenbildes auf seine Bildbreite ab. Im Fall der Makrokamera befindet sich der Film oder CCD-Chip in der Ebene des Zwischenbildes. Ist die Breite des lichtempfindlichen Bereichs L, dann wird eine Länge l des Objektes mit

l = L/m = F*f/x

darauf abgebildet. Der letztendliche Abbildungsmaßstab bzw. die Vergrößerung hängen davon ab, wie groß das Bild dem Betrachter präsentiert wird.

Ähnlich ist die Situation bei Aufnahme des Zwischenbildes durch ein Okular oder anderen Adapter. Mit Hilfe eines Okularmikrometers kann man leicht die Breite des Zwischenbildes (Sehfeld) bestimmen, die bei einer bestimmten Kamerabrennweite erfasst wird. Montiert man eine Coolpix 990 unmittelbar auf ein 8x-Okular des MBS-10, so ist das Bild etwa ab einer Brennweite von 18mm frei von Vignettierung. Ein fotografiertes Okularmikrometer zeigt dann ein Sehfeld mit einer Breite von L=12mm an. Die Größe im Objektraum ergibt sich wieder nach obigem Ausdruck als L/m. Bei dieser Brennweite verhält sich die Kamera nicht anders, als ein direkt belichteter Chip der Breite 12mm.