Konvergenzwinkel
Die nachfolgende Anleitung lehnt sich an die Ableitung der Berechnung der Stereobasis bei Nah- und Makroaufnahmen in "Stereo-Fotografie und Raumbild-Projektion" von G. Kuhn an.

Betrachtet sei ein Objekt der Tiefe T, das als graues Rechteck in der nebenstehenden Zeich-nung dargestellt ist. W bezeichnet den Fernpunkt, N den Nahpunkt. Es werde einmal von einer Kamera links oben aufgenommen und ein zweites Mal von einer Kamera, die um den Konvergenz-winkel β um den Nahpunkt N gedreht wurde. Dieser Winkel ist in der Zeichnung bewusst etwas übertrieben dargestellt. Die Entfernung der beiden Kamerapositionen vom Nahpunkt N ist die Nahpunktweite n. Die Kameras sind durch ihre Objektive (Linsen) und Bildebenen grafisch repräsentiert und haben die Brennweite f.

Im Falle der Betrachtung durch ein optisches System mit Unendlichoptik (Stereomikroskop nach dem Fernrohrprinzip) wird das dargestellte "Kameraobjektiv" gebildet durch das Objektiv des Stereomikroskops, die Tubuslinse und ggf. das zwischengeschaltete Galilei-System. Die Brennweite f hängt von den Brennweiten aller beteiligten Teilsysteme ab. Die Nahpunktweite n stimmt mit der Brennweite f_O des Objektivs des Stereomikroskops überein, wenn der Nahpunkt scharf abgebildet wird. Die in der Zeichnung dargestellte Bildebene wird mit dem Okular betrachtet oder über eine weitere abbildende Optik in die Bildebene einer Kamera abgebildet.

Bei der linken Kamera fallen die Bilder von W und N (genannt W' und N') zusammen, während W' und N' in der Ebene des reellen Bildes der zweiten Kamera um die Länge v differieren. Dies ist gerade die maximale Deviation bei der angenommenen Geometrie.

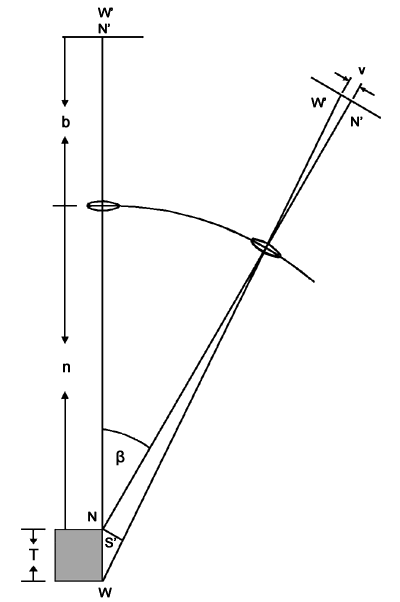
Zur Berechnung von v wird zunächst die Strecke S' ermittelt. Sie lässt sich exakt berechnen und anschließend unter den gegebenen typischen Längenverhältnissen vereinfachen. Da es mir hier nur um die Plausibilität geht, möchte ich einen anderen Weg beschreiten. Man kann unter der Kenntnis, dass n>> T ist, aus der Zeichnung die Näherung ablesen:

S' = T*sin(β)

Dazu muss man lediglich die Zentralprojektion durch eine Parallelprojektion annähern.

Für die hier behandelte Anwendung ist es vorteilhaft, den Abbildungsmaßstab k einzuführen:

k = v/S'

Damit ergibt sich für die Deviation die Formel:

v = k*T*sin(β)

Die praktischen Konvergenzwinkel bewegen sich in einem Bereich bis zu 15°, so dass man eine brauchbare Näherung durch lineare Näherung des Sinus erhält. Wird β in Grad angegeben, so wird daraus:

v = k*T*β*π/180°

Maximaler Konvergenzwinkel
Nach einer oft angewandten Erfahrungsregel soll die Deviation 1/30 der Bildbreite nicht übersteigen. Wird aus der Bildebene ein Ausschnitt der Breite D von der Kamera erfasst und wiedergegeben (z.B. 12mm bei einer Coolpix 990 auf einen 8x/23-Okular), dann lautet die Bedingung

v < D/30

mit obigem Ausdruck für v:

k*T*β*π/180°< D/30

Im Grenzfall der Gleichheit wird der maximale Konvergenzwinkel in Grad:

β_m = 6*D/(k*T*π)

Ist der Konvergenzwinkel β fest, so können maximale Tiefen T_m ereicht werden, wobei:

T_m = 6*D/(k*β*π)

Anmerkung zur Stereobasis
Wie in der Makrofotografie kann man auch mit der Stereobasis S arbeiten. Sie ist der Abstand der beiden Kameraobjektive im obigen Bild (S ist nicht eingezeichnet). Für kleine Winkel β gilt genähert:

S = n*sin(β)

Damit kann man aus der oben abgeleiteten Beziehung v = k*T*sin(β) den Konvergenzwinkel eliminieren und erhält:

v = k*T*S/n

Zum gleichen Ergebnis gelangt man, wenn man in der bei G. Kuhn (siehe Literaturhinweis) abgeleiteten Beziehung:

S = (v/k)*(n/T + 1)

wieder n>> T verwendet.

zurück