Gebrauch der Blende

Auf die Bedeutung der Blende für die Fotografie am Photomakroskop wurde bereits in der Einführung hingewiesen. Weil dieser Punkt von zentralem Interesse gerade in der Makrofotografie ist, soll er an dieser Stelle näher besprochen werden. Die numerische Apertur und die Auflösung bei visueller Beobachtung sind weiterhin Gegenstand dieser Seite. 


Geometrische Schärfentiefe
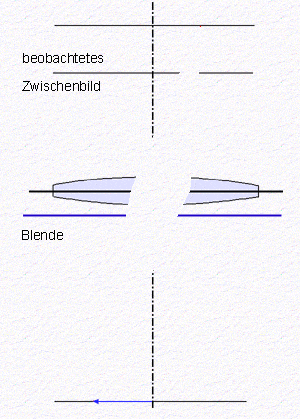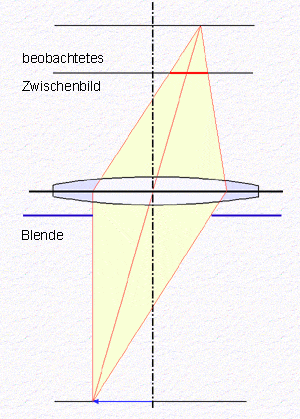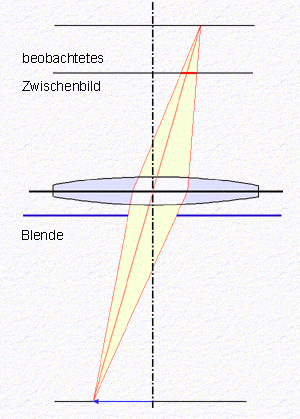
Ein Objektiv bildet Punkte einer Gegenstandsebene in Punkte einer Bildebene ab, wenn die Abbildungsgleichung (siehe Seite zum Abbildungsmaßstab) erfüllt ist. Ein realer Gegenstand liegt in der Regel nicht genau in einer Ebene, sondern besitzt eine räumliche Tiefe. Punkte des Objektes, die außerhalb der Gegenstandsebene liegen, werden vor oder hinter der Bildebene fokussiert. In der Bildebene, die beim Makroskop als Zwischenbildebene mit dem Okular betrachtet wird, erscheinen diese zu nahezu kreisförmigen Scheibchen aufgeweitet. Der begrenzende Kreis wird als Zerstreuungskreis bezeichnet. Die überlappenden Scheibchen führen in bestimmten Bildbereichen zu einem unscharfen Bildeindruck, wenn ihre Durchmesser einen tolerierbaren Wert (u) überschreiten. Umgekehrt erscheint das Objekt in seiner ganzen Tiefe scharf, wenn dieser Wert nirgends überschritten wird.

Da man den Durchmesser des Zerstreuungskreises auf das ganze betrachtete Bild beziehen muss, wächst er mit dem Aufnahmeformat. Werte für u wurden für verschiedenen Aufnahmeformate definiert, etwa 0,03mm für das Kleinbildformat. Als Richtwert kann man 1/1000 der Breite des Aufnahmeformats wählen. Bei der beschriebenen Anpassung der Kamera Coolpix 990 über ein Okular des MBS-10 wird zum Beispiel bei einer Brennweite der Kamera von 18mm ein Bereich des Zwischenbildes aufgenommen, das eine Breite von 12mm besitzt. Da das  gerade 1/3 der Breite des Kleinbildformates ist, darf der Durchmesser des Zerstreuungskreises auch nur etwa 0,01mm betragen. Neben der Tiefe des Objektes hängt der Wert u auch von der gewählten Blende ab. Im Bild rechts liegt ein Objekt (blauer Pfeil) näher am Brennpunkt, als die Gegenstandsebene. Er wird deshalb oberhalb der betrachteten Zwischenbildebene fokussiert. Der Durchmesser des Zerstreuungskreises in der Ebene des Zwischenbildes ist durch die Länge der rot markierten Strecke in der Zwischenbildebene gegeben. Das Bild zeigt alternierend zwei Blendeneinstellungen. Offensichtlich verkleinert sich der Zerstreuungskreis beim Abblenden. Durch Abblenden kann man deshalb die Schärfentiefe erhöhen.

Zur Illustration ist links eine kleine Blüte (ca. 4mm breit) mit unterschiedlichen Blenden aufgenommen. Die Blendenwerte k = f/d  mit: f  = Brennweite d = Durchmesser der Eintrittspupille sind rechts unten im Bild angegeben. Besser aufgelöste Einzelbilder zu diesem und einem weiteren Beispiel finden Sie hier.

Obwohl ich sehr für das pragmatische Ausprobieren von verschiedenen Blenden plädiere, halte ich es doch für nützlich, den Zusammenhang zwischen Blende und geometrischer Schärfentiefe zu kennen. Die scharf dargestellte Tiefe eines Motivs, also seine Schärfentiefe T ist gegeben durch:

Dabei bedeuten die Abkürzungen:
T = Abstand zwischen Fernpunkt (weitester scharf abgebildeter Punkt) und Nahpunkt (nächster scharf abgebildeter Punkt). Fernpunkt und Nahpunkt liegen jeweils  t=T/2 von der Gegenstandsweite entfernt.
k = Blende
u = Durchmesser des Zerstreuungskreises
m = Abbildungsmaßstab
p = Pupillenmaßstab = Durchmesser der Austrittspupille/ Durchmesser der Eintrittspupille

Dieser relativ einfache Ausdruck setzt voraus, dass der Abbildungsmaßstab m groß im Vergleich zu k*u/f ist. Er ist deshalb nur für Makroaufnahmen anwendbar.

Der Pupillenmaßstab kann grob gemessen werden. Dazu schließt man die Blende des Objektivs leicht, so dass man ihren Rand gut erkennen kann, und betrachtet das Objektiv aus einigem Abstand.  Mit Hilfe einer Schieblehre misst man den scheinbaren Durchmesser der Blende von beiden Seiten des Objektivs und berechnet das Verhältnis der Werte. Bei den empfohlenen Makroobjektiven, Balgenköpfen, Vergrößerungsobjektiven und den vielen Normalobjektiven handelt es sich um symmetrische Objektive, so dass hier einfach p=1 gilt.

Sucht man zu einer gegebenen Tiefe die erforderliche Blende, so löst man obige Formel nach k auf:

Unschärfe durch Beugung
Leider kann man das Problem geringer Schärfentiefe nicht generell durch Abblenden lösen. Denn, je kleiner man die Öffnung macht, desto größer wird die Unschärfe durch die Beugung an der Eintrittspupille, wie es bereits im Abschnitt zur visuellen Beobachtung diskutiert wurde. Setzt man den Ausdruck für die numerische Apertur

in die Formel für die Größe des Airyschen Beugungsscheibchens in der Zwischenbildebene:

ein, so erhält man folgende Beziehungen:

und daher

Diese Ausdrücke beantworten die Frage, welche Größe das Beugungsscheibchen bei einer gegebenen Blende annimmt, bzw., welche Blende man bei einer akzeptierten Größe des Beugungsscheibchens wählen muss. Legt man das Rayleigh-Kriterium zugrunde, dann gibt die erste Formel auch an, ab welchem Punktabstand im Zwischenbild zwei inkohärent leuchtende Punkte trennbar sind. Die zweite erlaubt eine Berechnung der zur Trennung erforderlichen Blende.
 

Förderliche Blende
Kurz zusammengefasst kann man sagen, dass sich die Schärfentiefe zwar durch Abblenden beliebig vergrößern lässt, aber die mit dem Blendenwert linear wachsenden Beugungsscheibchen ab einem bestimmten Blendenwert zu einer Verschlechterung der gesamten Schärfe führen.

Die so genannte "förderliche Blende" ist ein Kompromiss, der einerseits die Unschärfe in Folge der Beugung auf ein erträgliches Maß begrenzt, anderseits eine relativ hohe Schärfentiefe ermöglicht. Üblicherweise findet sich in der Literatur folgende Formel für die förderliche Blende k_f:

Dabei ist u wieder der noch zulässige Durchmesser des Zerstreuungskreises. Man erkennt, dass man zu diesem Ausdruck gelangt, wenn man nach dem Rayleigh-Kriterium den Abstand auflösbarer Punkte zu u wählt. Mit anderen Worten: Zwei Punkte, die voneinander den Abstand des Durchmessers des Zerstreuungskreises haben, liegen bei der förderlichen Blende an der Grenze der Trennbarkeit. Damit sind bei der üblichen Festlegung des Wertes von u ca. 1000 Punkte in der Bildbreite auflösbar, sofern sie in der Schärfeebene liegen.

Die einzige logische Verknüpfung zwischen Beugung und Schärfentiefe besteht in der Größe u. Der Blendenwert wird so groß gewählt, dass gerade die Beugungseffekte noch nicht eklatant ins Auge fallen. Die Schärfentiefe ist dann maximal im dem Sinne, dass eine weitere Erhöhung der Schärfentiefe (und damit des Blendenwertes) das Bild in allen Teilen sichtbar verschlechtern würde.

Die Berechnung lässt sich noch etwas vereinfachen, indem man für die Wellenlänge λ=550nm einsetzt. Gibt man u in Millimetern an, so erhält man gerundet:

Beispiele: Beim Kleinbildformat  und einem Abbildungsmaßstab von 1:1 (m=1) erhält man eine förderliche Blende von etwa 22. Ist dagegen der Abbildungsmaßstab von 5:1 (m=5) ist der Blendenwert etwas unterhalb von 8.

Ich halte die Anwendung der förderlichen Blende in einigen Fällen für suboptimal und betrachte sie primär als äußerste Grenze, über die hinaus man nicht abblenden sollte. Dies sind die Gründe: 

Der noch akzeptierte Radius des Beugungsscheibchens wird als Durchmesser des Zerstreuungskreises gewählt. Dies bedeutet, dass die Beugung bereits an der Grenze der Erkennbarkeit liegt.

In Bildbereichen, bei denen das Objekt auf Grund seiner Tiefe nicht exakt scharf abgebildet wird, kommt zur Beugungsunschärfe noch der Zerstreuungskreis hinzu. In einem einfachen Modell kann man davon ausgehen, dass sich die Radien des Beugungsscheibchens und des Zerstreuungskreises addieren.

Die wirkliche Tiefe des Objektes geht nicht in die Berechnung der förderlichen Blende ein. Es wird deshalb kein Optimum für ein gegebenes Motiv bestimmt. Das kann man sich leicht an einem Beispiel veranschaulichen: Ist das Motiv nahezu eben, wie etwa eine geschliffene Steinoberfläche oder ein Farbdruck auf Papier, so ist der Zerstreuungskreis in Folge der geringen Objekttiefe extrem klein. Selbst mit weit geöffneter Blende kann man ein überall scharfes Bild aufnehmen. Wählt man aber die förderliche Blende, so blendet man unnötig ab und nimmt eine Reihe von Nachteilen in Kauf:

• Die Beugungsunschärfe ist so hoch, dass keine Ausschnittsvergrößerung mehr möglich ist.

• Die Belichtungszeit und damit die Gefahr des Verwackelns steigen unnötig.

• Das Signal/Rausch-Verhältnis verschlechtert sich (Bildrauschen).

Aussagen, die förderliche Blende sei ein Optimum hinsichtlich der Unschärfe durch Tiefe des Objektes und Beugungsunschärfe, möge man vor diesem Hintergrund kritisch betrachten.

Ist es erwünscht, die Schärfentiefe zu erhöhen, besteht neben dem Abblenden die Möglichkeit, mehrere Schärfeebenen aufzunehmen und zu einem scharfen Bild zu kombinieren. Auf diese Möglichkeit wurde bereits hingewiesen. Gerade bei einem Makroskop mit seinem axialen Aufbau bietet sich diese Alternative an.

An einer Stelle bin ich auf eine abweichende Berechnungsformel der förderlichen Blende gestoßen. In dem Buch "Makro Fotografie" von Richard Hünecke und Thomas Maschke findet sich der Ausdruck:

Auch die Tabellen in diesem Buch sind so kalkuliert. Ich halte den Vorfaktor 1000 für etwas besser geeignet, als den üblichen Faktor. Joachim Inkmann hat mich darauf hingewiesen, dass der Begriff der „förderlichen Blende“ aus dem Aufsatz „Die “förderliche Blende” bei Makroaufnahmen“ von Hermann Eisenbeiss stammt (Zeitschrift: International Photo Technik, 4, 1967, 296ff). Der Autor geht von einer mittleren Wellenlänge von 600nm aus. Damit ergäbe sich ein Vorfaktor von 1366, der recht großzügig abgerundet wird. Vor dem Hintergrund der heuristischen Ableitung der förderlichen Blende erscheint mir die Näherung legitim.

Bei Einhaltung der förderlichen Blende muss man sich bei modernen Digitalkameras meist wenig Gedanken darüber machen, ob die Kameraauflösung ausreichend ist. Da man den Wert des Unschärfekreises zu etwa 1/1000 der Breite des Aufnahmeformats definiert und dies bei der förderlichen Blende der Auflösung entspricht, benötigt man in der Breite ca. 2000 Pixel. Dann sind nach dem Nyquist-Kriterium 1000 Punkte auflösbar. Viele Kameras werden noch Auflösungsreserven übrig haben, die bei kleineren Blendenwerten gegebenenfalls nutzbar sind.

Zur Frage nach einer optimalen Blende, die Beugung und Tiefe des Objekts explizit berücksichtigt, habe ich eine kurze Notiz geschrieben.